Hint: Read the Vectors Tips page - these could come in handy!

Write functions

Here are a bunch of functions you should be able to write. Any of these may appear (directly or modified) on a quiz or exam! Your function should be able to pass the test functions provided.

for loops

Sum from m to n

There are many ways to sum the integers between two bounds, m and n.

a) loopSumFromMToN(m, n)

Use a for loop to sum the total of the integers between m and n.

testLoopSumFromMToN <- function() {
    cat("Testing loopSumFromMToN()...")
    stopifnot(loopSumFromMToN(5, 10) == (5+6+7+8+9+10))
    stopifnot(loopSumFromMToN(1, 1) == 1)
    stopifnot(loopSumFromMToN(0, 0) == 0)
    stopifnot(loopSumFromMToN(0, 7) == (1+2+3+4+5+6+7))
    cat("Passed!\n")
}

b) vectorSumFromMToN(m, n)

Use a vector (no loops!) to sum the total of the integers between m and n.

testVectorSumFromMToN <- function() {
    cat("Testing vectorSumFromMToN()...")
    stopifnot(vectorSumFromMToN(5, 10) == (5+6+7+8+9+10))
    stopifnot(vectorSumFromMToN(1, 1) == 1)
    stopifnot(vectorSumFromMToN(0, 0) == 0)
    stopifnot(vectorSumFromMToN(0, 7) == (1+2+3+4+5+6+7))
    cat("Passed!\n")
}

c) formulaSumFromMtoN(m, n)

Use a closed formula (no vectors or loops!) to sum the total of the integers between m and n. Hint: Wikipedia is helpful :)

testFormulaSumFromMtoN <- function() {
    cat("Testing formulaSumFromMtoN()...")
    stopifnot(formulaSumFromMtoN(5, 10) == (5+6+7+8+9+10))
    stopifnot(formulaSumFromMtoN(1, 1) == 1)
    stopifnot(formulaSumFromMtoN(0, 0) == 0)
    stopifnot(formulaSumFromMtoN(0, 7) == (1+2+3+4+5+6+7))
    cat("Passed!\n")
}

d) sumEveryKthFromMToN(m, n, k)

Use a for loop to sum every kth integer between m and n.

testSumEveryKthFromMToN <- function() {
    cat("Testing sumEveryKthFromMToN()...")
    stopifnot(sumEveryKthFromMToN(5, 20, 7) == (5 + 12 + 19))
    stopifnot(sumEveryKthFromMToN(1, 10, 2) == (1 + 3 + 5 + 7 + 9))
    stopifnot(sumEveryKthFromMToN(0, 0, 1) == 0)
    cat("Passed!\n")
}

e) sumOfOddsFromMToN(m, n)

Use a for loop to sum every odd integer between m and n.

testSumOfOddsFromMToN1 <- function() {
    cat("Testing sumOfOddsFromMToN1()...")
    stopifnot(sumOfOddsFromMToN1(4, 10) == (5 + 7 + 9))
    stopifnot(sumOfOddsFromMToN1(5, 9) == (5 + 7 + 9))
    cat("Passed!\n")
}

fizzBuzz()

The “Fizz-Buzz test” is a classic interview question for programming job candidates. Write a function that prints the numbers from 1 to 100 (with each number on a new line), but for multiples of 3 print “Fizz” instead of the number, and for multiples of 5 print “Buzz”. For numbers which are multiples of both 3 and 5 print “FizzBuzz”. The first 16 lines of fizzBuzz() should read:

1
2
"Fizz"
4
"Buzz"
"Fizz"
7
8
"Fizz"
"Buzz"
11
"Fizz"
13
14
"FizzBuzz"
16

while loops

nthMultipleOf4Or7(n)

Find the nth positive integer that is a multiple of either 4 or 7. Hint: you should write a helper function called isMultipleOf4Or7(n) that returns TRUE if n is a multiple of 4 or 7 and FALSE otherwise.

testNthMultipleOf4Or7 <- function() {
    cat("Testing nthMultipleOf4Or7()...")
    stopifnot(nthMultipleOf4Or7(1) == 4)
    stopifnot(nthMultipleOf4Or7(2) == 7)
    stopifnot(nthMultipleOf4Or7(3) == 8)
    stopifnot(nthMultipleOf4Or7(4) == 12)
    stopifnot(nthMultipleOf4Or7(5) == 14)
    stopifnot(nthMultipleOf4Or7(6) == 16)
    stopifnot(nthMultipleOf4Or7(10) == 28)
    cat("Passed!\n")
}

Prime Numbers

Background: Read up on the Wikipedia page on prime numbers. We want to write the function nthPrime(n). However, to write that function, we’ll first need to write isPrime(n), which determines whether a number is prime or not.

a) isPrime(n)

Write the function isPrime(n) which takes a non-negative integer, n, and returns TRUE if it is a prime number and FALSE otherwise.

testIsPrime <- function() {
    cat("Testing isPrime()...")
    stopifnot(isPrime(1) == FALSE)
    stopifnot(isPrime(2) == TRUE)
    stopifnot(isPrime(7) == TRUE)
    stopifnot(isPrime(13) == TRUE)
    stopifnot(isPrime(14) == FALSE)
    cat("Passed!\n")
}

b) nthPrime(n)

Write the function nthPrime(n) which takes a non-negative integer, n, and returns the nth prime number, where nthPrime(1) returns the first prime number (2).

testNthPrime <- function() {
    cat("Testing nthPrime()...")
    stopifnot(nthPrime(1) == 2)
    stopifnot(nthPrime(2) == 3)
    stopifnot(nthPrime(3) == 5)
    stopifnot(nthPrime(4) == 7)
    stopifnot(nthPrime(7) == 17)
    cat("Passed!\n")
}

Turtle loops!

turtleCircleInSquare(s)

Write the function turtleCircleInSquare(s) that uses the TurtleGraphics library to draw a circle inscribed inside a square with side s < 100. The square and circle should be centered in the turtle’s terrarium. Hint: You may want to use turtleSquare(s) and turtleCircle(r) as helper functions! The following code should produce a circle inscribed inside a square with a side length of 50:

library(TurtleGraphics)
turtle_init()
turtle_do({
    turtleCircleInSquare(50)
})

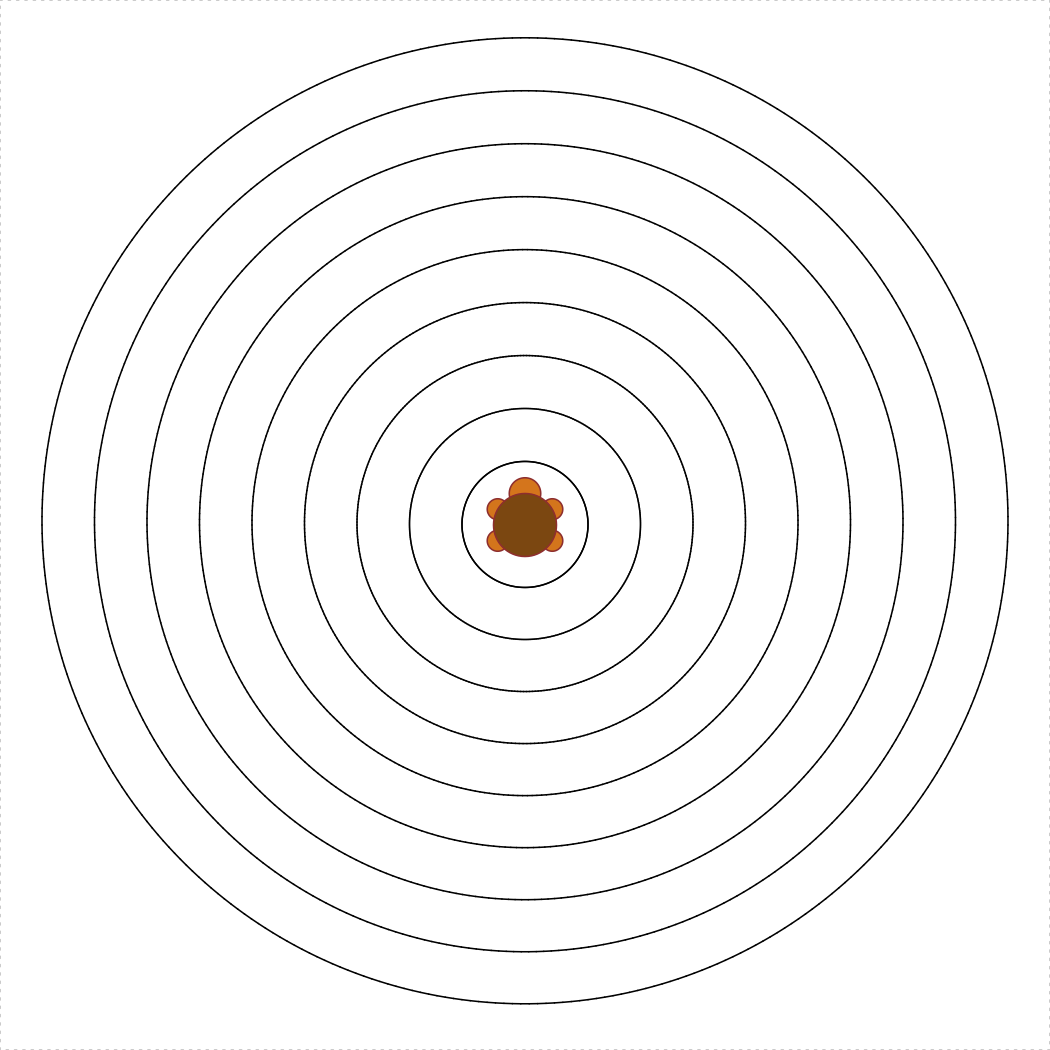
concentricTurtleCircles(spacing = 5)

Write the function concentricTurtleCircles(spacing) that uses the TurtleGraphics library to draw concentric circles from the center of the terrarium and outward. The spacing argument determines the spacing between each circle, and the default value should be spacing = 5. Also, spacing >= 1, and your function must not allow the turtle to escape the terrarium. Hint: you may want to use turtleCircle(r) as a helper function. The following code should produce concentric circles with a spacing of 5:

library(TurtleGraphics)
turtle_init()
turtle_do({
    concentricTurtleCircles()
})

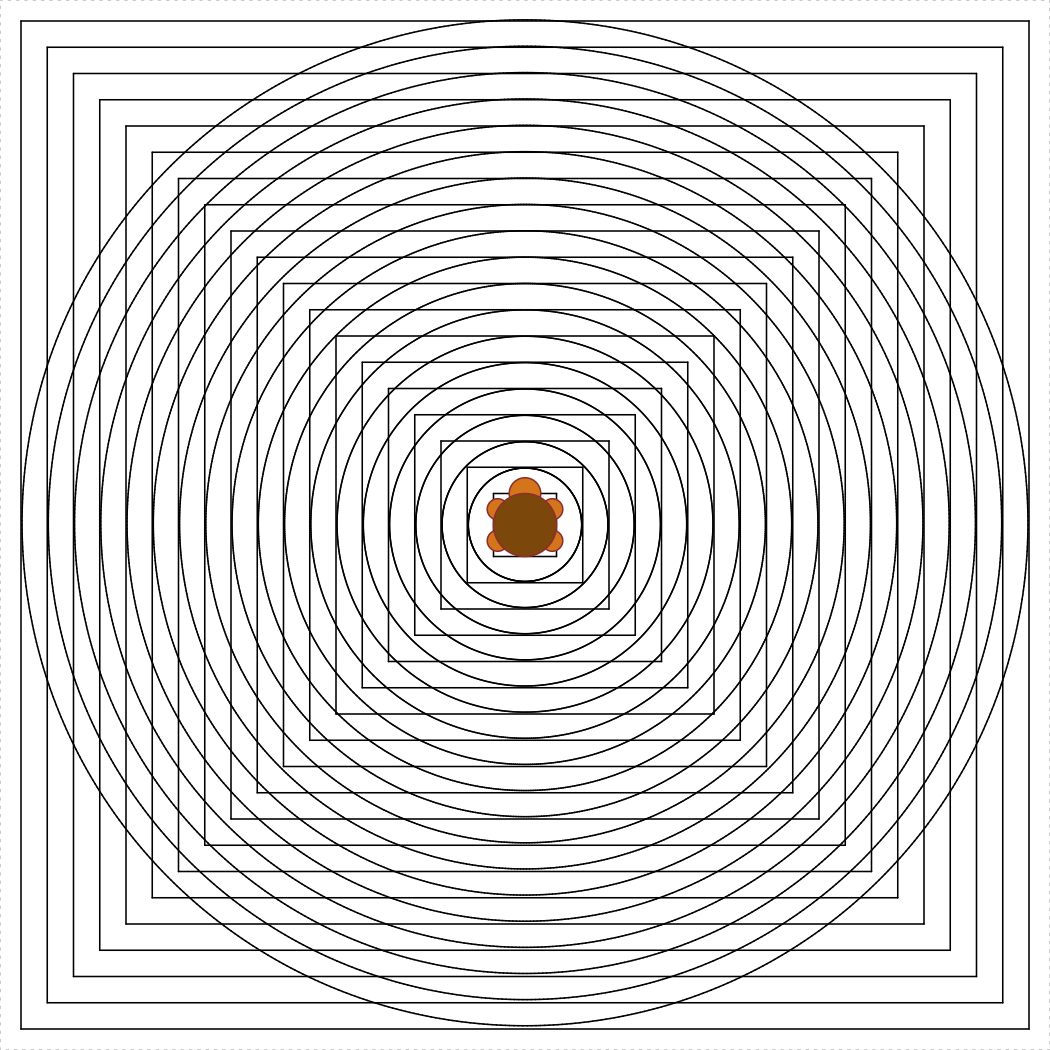
concentricTurtleCircleInSquares(spacing = 5)

Write the function concentricTurtleCircleInSquares(spacing) that uses the TurtleGraphics library to draw concentric circles inscribed in squares from the center of the terrarium and outward. The spacing argument determines the spacing between each circle, and the default value should be spacing = 5. Also, spacing >= 1, and your function must not allow the turtle to escape the terrarium. Hint: you may want to use turtleCircleInSquare(s) as a helper function. The following code should produce concentric circles inscribed in squares with a spacing of 5:

library(TurtleGraphics)
turtle_init()
turtle_do({
    concentricTurtleCircleInSquares()
})

Page sources:

Some content on this page has been modified from other courses, including:

EMSE 6574, Sec. 11: Programming for Analytics (Fall 2019)
George Washington University | School of Engineering & Applied Science
Dr. John Paul Helveston | jph@gwu.edu | Mondays | 6:10–8:40 PM | Phillips Hall 108 | |
This work is licensed under a Creative Commons Attribution 4.0 International License.
See the licensing page for more details about copyright information.
Content 2019 John Paul Helveston