Homework 3 - Loops & Vectors
Due: Sunday, 06-Oct. at 8pm
Rules:
- Problems marked SOLO may not be worked on with other classmates, though you may consult instructors for help.
- For problems marked COLLABORATIVE, you may work in groups of up to 3 students who are in this course this semester (and then with nobody else except the course instructors). You may not split up the work – everyone must work on every problem. And you may not simply copy any code but rather truly work together.
- Even though you work collaboratively, you still must submit your own solutions.
Instructions:
Before beginning this assignment, be sure to have read the Loops and Vectors lessons.
Open RStudio and create a new project called “hw3-lastName”, replacing “lastName” with your last name.
Download the hw3.R template script and place it in RStudio project folder you just created.
Fill out your name, GW Net ID, and the names of anyone you worked with in the header of the “hw3.R” file.
Type all of your answers to the questions below in the “hw3.R” script.
After completing the questions, create a zip file of all files in your R project folder for this assignment.
Submit the zip file on Blackboard by the due deadline.
Write solutions to the following functions in your “hw3.R” script.
Rules:
- You may only use strings for problem #3 (which requires printing a string to the screen). On all other problems you may NOT use strings.
1) loopFactorial(n) [SOLO, 5 pts]
Use a for loop to write the function
loopFactorial(n) that should return n!,
i.e. “n factorial”, which is defined for all non-negative integers. For
example, 3! = 3*2*1 = 6, 4! = 4*3*2*1 = 24,
and 5! = 5*4*3*2*1 = 120. Note that 0 is a
special case, and 0! = 1. Assume
n >= 0.
2) vectorFactorial(n) [SOLO, 5 pts]
Write the function vectorFactorial(n), which again
computes the factorial of n but use vectors to avoid using
a loop. Hint: there are some useful functions listed on the vectors lesson page for
performing operators on a vector.
3) printStarTriangle(n) [SOLO, 10 pts]
Write a function that prints a triangle of asterisks (*)
where the number of asterisks in each row is equal to the row number.
So, printStarTriangle(5) should print out:
*
**
***
****
*****4) nthHighestValue(n, x) [SOLO, 10 pts]
Write a function to find the nth highest value in a given vector. For
example, if x equals c(5, 1, 3), then
nthHighestValue(1, x) should return 5, because
5 is the 1st highest value in x, and
nthHighestValue(2, x) should return 3 because
it’s the 2nd highest value in x. Assume only numeric
inputs, and assume that n <= length(x). You may not use
loops.
5) numDigits(n) [SOLO, 10 pts]
Write the function numDigits(n) that takes a
possibly-negative integer and returns the number of digits in
it. So, numDigits(12345) returns 5,
numDigits(0) returns 1, and
numDigits(-111) returns 3. One way you could
solve this is to convert n to a string and use
str_length(), but you cannot do that since you may not use
strings here. This can also be solved with logarithms, but seeing as
this is “loops week”, you should instead simply repeatedly remove the
ones digit until you run out of digits.
6) Happy Numbers [COLLABORATIVE]
Background: Read the first paragraph from the Wikipedia page on
happy numbers. After some thought, we see that no matter what number we
start with, when we keep replacing the number by the sum of the squares
of its digits, we’ll always either arrive at 4 (unhappy) or at 1
(happy). With that in mind, we want to write the function
nthHappyNumber(n). However, to write that function, we’ll
first need to write isHappyNumber(n), which determines
whether a number is “happy” or not. And to right that function, we’ll
first need to write sumOfSquaresOfDigits(n). And that’s
top-down design! Here we go…
a) sumOfSquaresOfDigits(n) [10 pts]
Write the function sumOfSquaresOfDigits(n) which takes a
non-negative integer, n, and returns the sum of the squares
of its digits (assume that n will always be a positive
integer, so no need to check for bad inputs).
b) isHappyNumber(n) [10 pts]
Write the function isHappyNumber(n) which takes a
possibly-negative integer and returns TRUE if it
is happy and FALSE otherwise. Note that all numbers less
than 1 are not happy.
c) nthHappyNumber(n) [10 pts]
Write the function nthHappyNumber(n) which takes a
non-negative integer, n, and returns the nth happy number,
where nthHappyNumber(1) returns the first happy number (1).
7) Turtle loops! [COLLABORATIVE]
a) turtleSquare(s) redux [5 pts]
Re-write the turtleSquare(s) function from HW2, but this time use a for
loop to draw the sides of the square. The following code should produce
a square with a side length of 50:
library(TurtleGraphics)
turtle_init()
turtle_do({
turtleSquare(50)
})
b) concentricTurtleSquares(spacing = 5) [10 pts]
Write the function concentricTurtleSquares(spacing) that
uses the TurtleGraphics library to draw concentric squares
from the center of the terrarium and outward. The spacing
argument determines the spacing between each square, and the default
value should be spacing = 5. Also,
spacing >= 1, and your function must not allow the
turtle to escape the terrarium. Hint: you may want to use
turtleSquare(s) as a helper function. The following code
should produce concentric squares with a spacing of 5:
library(TurtleGraphics)
turtle_init()
turtle_do({
concentricTurtleSquares()
})
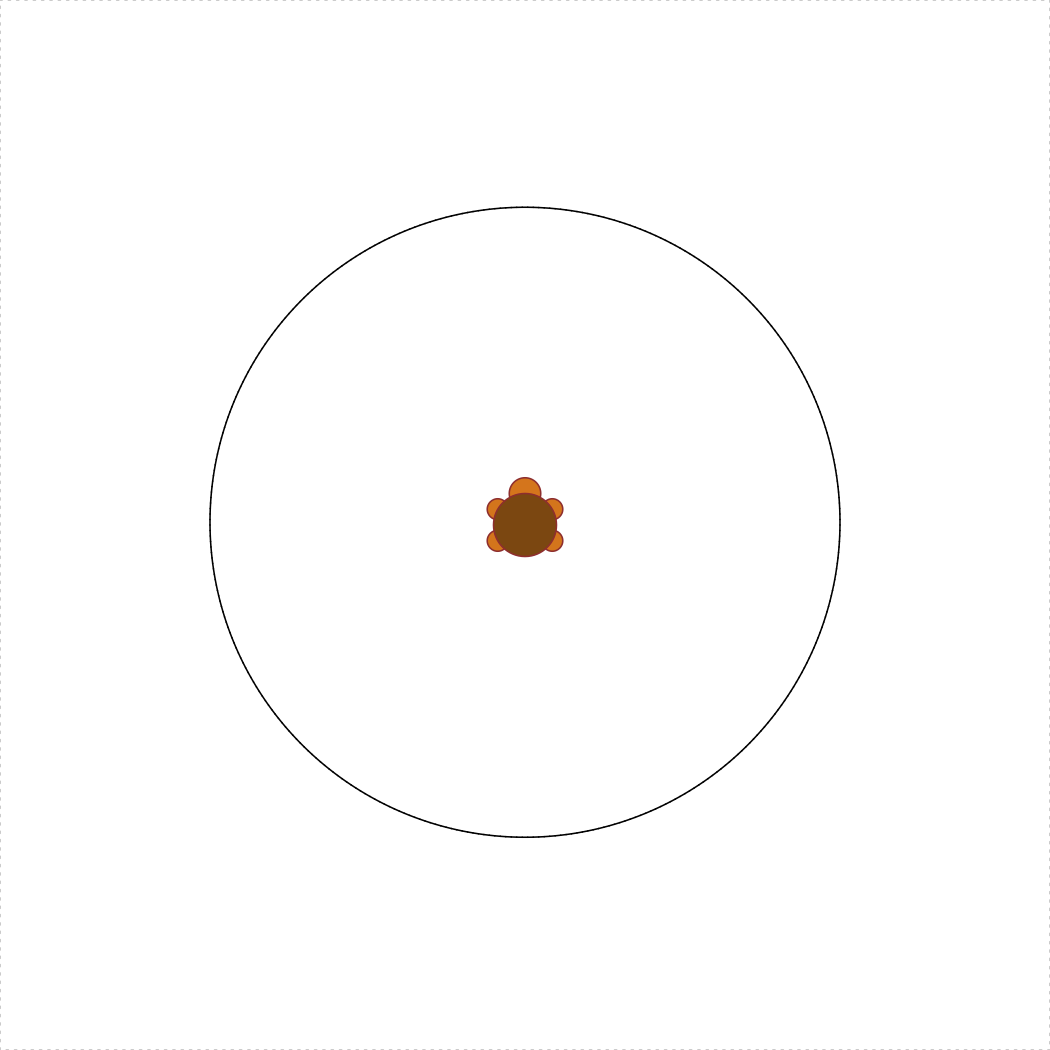
c) turtleCircle(r) [15 pts]
Write the function turtleCircle(r) that uses the
TurtleGraphics library to draw a circle with radius
r < 50. The circle should be centered in the turtle’s
terrarium. Hint: To get the circle centered, remember that a circle has
360 degrees, and the circumference of a circle is \(2\pi r\). The following code should produce
a circle with a radius of 30:
library(TurtleGraphics)
turtle_init()
turtle_do({
turtleCircle(30)
})
Bonus Credit 1) turtleSquareRotated(s, degrees) [SOLO,
2.5 pts]
Write the function turtleSquareRotated(s, degrees) that
uses the TurtleGraphics library to draw a square with side
length s < 100 and rotated by
degrees <= 180 counterclockwise from the horizontal
plane. The rotated square should be centered in the turtle’s terrarium.
Hint: you’re going to need to use the cosine (cos()) and
sine (sin()) functions; in R, these functions take angles
in radians (not degrees), so remember to convert your
angles (180 degrees = \(\pi\)). The
following code should produce a square with a side length of 30 and
rotated by 30 degrees:
library(TurtleGraphics)
turtle_init()
turtle_do({
turtleSquareRotated(30, 30)
})
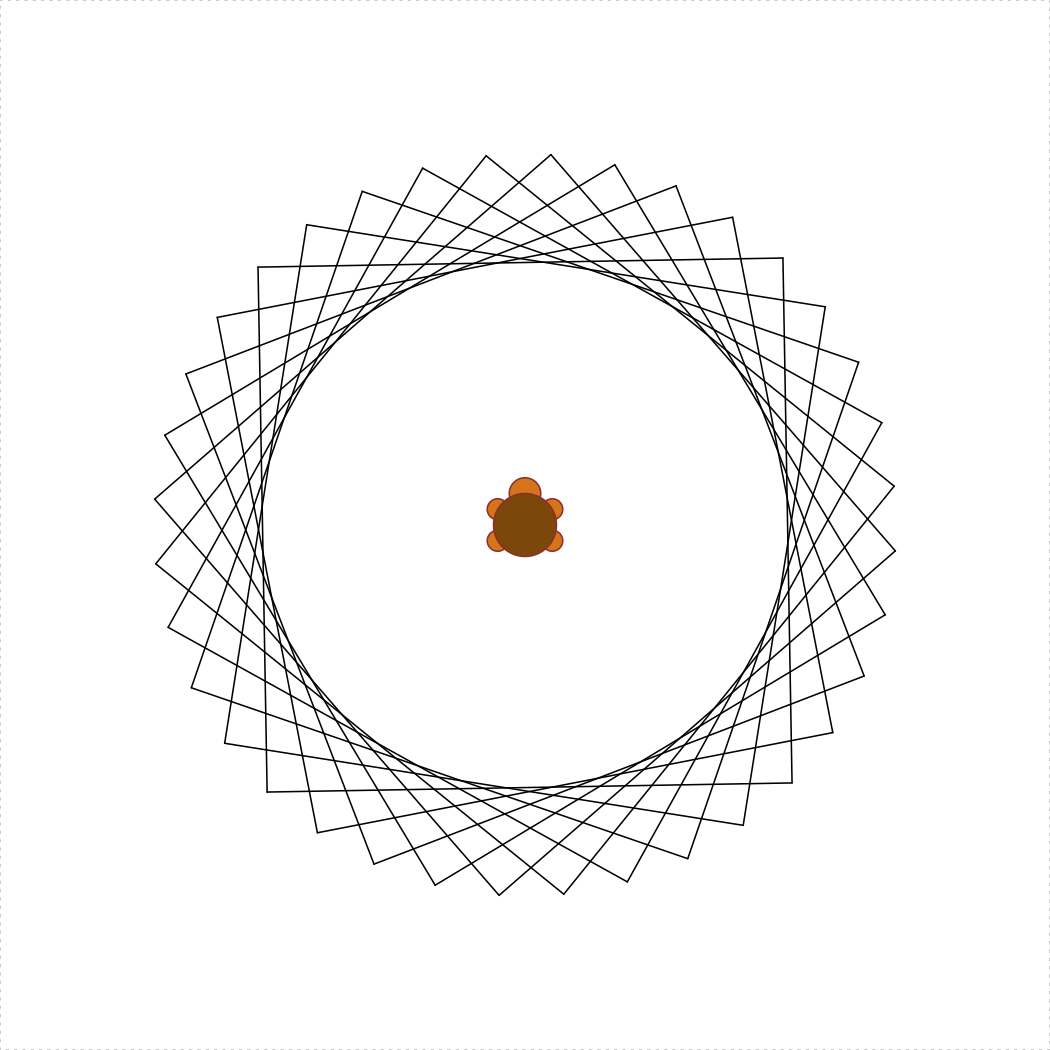
Bonus Credit 2) turtleSquareStar(s, degreeSpacing = 20)
[SOLO, 2.5 pts]
Write the function turtleSquareStar(s, degreeSpacing)
that uses the turtleSquareRotated(s, degrees) as a helper
function to draw a sequence of overlapping rotated squares with side
length s < 70 to form a star. The
degreeSpacing argument determines the spacing in degrees
between each rotated square, and the default value should be
degreeSpacing = 20. Also,
1 <= degreeSpacing <= 60, and your function must not
allow the turtle to escape the terrarium. The following code should
produce the star of rotated squares with a side length of 50 and 20
degree spacings between each square:
library(TurtleGraphics)
turtle_init()
turtle_do({
turtleSquareStar(50, 20)
})
Page sources:
Some content on this page has been modified from other courses, including:
George Washington University | School of Engineering & Applied Science
Dr. John Paul Helveston | jph@gwu.edu | Mondays | 6:10–8:40 PM | Phillips Hall 108 | |
This work is licensed under a Creative Commons Attribution 4.0 International License.
See the licensing page for more details about copyright information.
Content 2019 John Paul Helveston